Time Evolution using Renormalizer

Overview

In this notebook we will simulate the charge transfer between two molecules using the Marcus model

\[\hat H = -V(a^\dagger_0 a_1 + a^\dagger_1 a_0) + \Delta G a^\dagger_1 a_1 + \omega \sum_{i=0, 1} b^\dagger_i b_i + g \omega \sum_{i=0, 1} a^\dagger_i a_i (b^\dagger_i + b_i)\]

with transfer integral \(V=-0.1\), dimensionless coupling constant \(g=1\), vibration frequency \(\omega=0.5\).

We will first show how to use Renormalizer to simulation the time evolution at \(\Delta G = 0\). Then, we will show that, by decreasing the reaction Gibbs free energy change \(\Delta G\), the reaction rate will first increase and then decrease, as predicted by the Marcus theory.

Preparation: Setting Up Logger

from renormalizer.utils.log import package_logger as logger

2025-12-20 11:02:59,619[INFO] Use NumPy as backend
2025-12-20 11:02:59,620[INFO] numpy random seed is 9012
2025-12-20 11:02:59,621[INFO] random seed is 1092
2025-12-20 11:02:59,631[INFO] Git Commit Hash: 06430a9cbb7af930317f368a36eff512a8d5ce70
2025-12-20 11:02:59,632[INFO] use 64 bits

logger.debug("logger output")

2025-12-20 11:02:59,669[DEBUG] logger output

from renormalizer.utils.log import set_stream_level, INFO

# filter logger output
set_stream_level(INFO)

logger.debug("This message will not be shown")

logger.info("Logger output")

2025-12-20 11:02:59,688[INFO] Logger output

Define the Model and Initial State

from renormalizer import Op, BasisMultiElectron, BasisSHO, Model
import numpy as np

v = -0.1
g = 1
omega = 0.5
nbas = 16

def get_model(delta_g):
    ham_terms = v * Op(r"a^\dagger a", ["e0", "e1"]) + v * Op(r"a^\dagger a", ["e1", "e0"])
    ham_terms += delta_g * Op(r"a^\dagger a", "e1")
    for i in range(2):
        ham_terms += omega * Op(r"b^\dagger b", f"v{i}")
        ham_terms += g * omega * Op(r"a^\dagger a", f"e{i}") * Op(r"b^\dagger+b", f"v{i}")
    basis = [BasisMultiElectron(["e0", "e1"], [0, 0]), BasisSHO("v0", omega, nbas), BasisSHO("v1", omega, nbas)]
    return Model(basis, ham_terms)

# using a relaxed initial state
def get_init_condition():
    basis = BasisSHO(0, omega, nbas)
    state = np.linalg.eigh(basis.op_mat(r"b^\dagger b") + g * basis.op_mat(r"b^\dagger+b"))[1][:, 0]
    return {"v0": state}
init_condition = get_init_condition()

Time Evolution with the Default Configuration

Next, we run the simulation using the evolve method in the Mps class. At this phase, we keep \(\Delta G = 0\).

delta_g = 0
model = get_model(delta_g)

from renormalizer import Mps, Mpo

# Hamiltonian MPO
mpo = Mpo(model)
# The occupation of e0
n_op = Mpo(model, Op(r"a^\dagger a", "e0"))

# initialize the MPS
mps = Mps.hartree_product_state(model, condition=init_condition)
# time evolution step
dt = 0.2
# record the electronic occupation
n_list = []
for i_step in range(50):
    n = mps.expectation(n_op)
    logger.info(f"Step {i_step}. Time {i_step * dt:.2f}. $n$ {n}")
    # perform time evolution. Note that the evolution is not in-place.
    mps = mps.evolve(mpo, dt)
    n_list.append(n)

2025-12-20 11:02:59,739[INFO] Step 0. Time 0.00. $n$ 0.9999999999999998
2025-12-20 11:02:59,752[INFO] Step 1. Time 0.20. $n$ 0.9996030537865594
2025-12-20 11:02:59,764[INFO] Step 2. Time 0.40. $n$ 0.998431396656162
2025-12-20 11:02:59,778[INFO] Step 3. Time 0.60. $n$ 0.9965532876450579
2025-12-20 11:02:59,793[INFO] Step 4. Time 0.80. $n$ 0.9940731362639054
2025-12-20 11:02:59,809[INFO] Step 5. Time 1.00. $n$ 0.9911161868842491
2025-12-20 11:02:59,825[INFO] Step 6. Time 1.20. $n$ 0.9878132450238745
2025-12-20 11:02:59,841[INFO] Step 7. Time 1.40. $n$ 0.9842873078294337
2025-12-20 11:02:59,856[INFO] Step 8. Time 1.60. $n$ 0.9806441927926955
2025-12-20 11:02:59,872[INFO] Step 9. Time 1.80. $n$ 0.976967746624379
2025-12-20 11:02:59,888[INFO] Step 10. Time 2.00. $n$ 0.9733182226560808
2025-12-20 11:02:59,904[INFO] Step 11. Time 2.20. $n$ 0.9697373081106376
2025-12-20 11:02:59,920[INFO] Step 12. Time 2.40. $n$ 0.9662497016753406
2025-12-20 11:02:59,936[INFO] Step 13. Time 2.60. $n$ 0.962867160945706
2025-12-20 11:02:59,951[INFO] Step 14. Time 2.80. $n$ 0.9595919026133962
2025-12-20 11:02:59,968[INFO] Step 15. Time 3.00. $n$ 0.9564197521679629
2025-12-20 11:02:59,984[INFO] Step 16. Time 3.20. $n$ 0.9533423734970323
2025-12-20 11:03:00,000[INFO] Step 17. Time 3.40. $n$ 0.9503492089387037
2025-12-20 11:03:00,016[INFO] Step 18. Time 3.60. $n$ 0.9474287391824951
2025-12-20 11:03:00,032[INFO] Step 19. Time 3.80. $n$ 0.9445692798814913
2025-12-20 11:03:00,048[INFO] Step 20. Time 4.00. $n$ 0.9417594196434944
2025-12-20 11:03:00,064[INFO] Step 21. Time 4.20. $n$ 0.9389883140168839
2025-12-20 11:03:00,081[INFO] Step 22. Time 4.40. $n$ 0.9362456942950406
2025-12-20 11:03:00,097[INFO] Step 23. Time 4.60. $n$ 0.9335221984937244
2025-12-20 11:03:00,113[INFO] Step 24. Time 4.80. $n$ 0.9308095732941701
2025-12-20 11:03:00,129[INFO] Step 25. Time 5.00. $n$ 0.9281008849250423
2025-12-20 11:03:00,146[INFO] Step 26. Time 5.20. $n$ 0.9253906107085343
2025-12-20 11:03:00,162[INFO] Step 27. Time 5.40. $n$ 0.9226738471654728
2025-12-20 11:03:00,178[INFO] Step 28. Time 5.60. $n$ 0.9199478805518423
2025-12-20 11:03:00,194[INFO] Step 29. Time 5.80. $n$ 0.9172094618331406
2025-12-20 11:03:00,211[INFO] Step 30. Time 6.00. $n$ 0.9144551950424458
2025-12-20 11:03:00,227[INFO] Step 31. Time 6.20. $n$ 0.9116816732036944
2025-12-20 11:03:00,243[INFO] Step 32. Time 6.40. $n$ 0.9088859026726781
2025-12-20 11:03:00,260[INFO] Step 33. Time 6.60. $n$ 0.9060659656334908
2025-12-20 11:03:00,276[INFO] Step 34. Time 6.80. $n$ 0.9032210121837198
2025-12-20 11:03:00,293[INFO] Step 35. Time 7.00. $n$ 0.9003515623906606
2025-12-20 11:03:00,309[INFO] Step 36. Time 7.20. $n$ 0.8974590790192766
2025-12-20 11:03:00,326[INFO] Step 37. Time 7.40. $n$ 0.8945453849965326
2025-12-20 11:03:00,342[INFO] Step 38. Time 7.60. $n$ 0.8916120979060871
2025-12-20 11:03:00,359[INFO] Step 39. Time 7.80. $n$ 0.8886602437062094
2025-12-20 11:03:00,376[INFO] Step 40. Time 8.00. $n$ 0.8856902107426247
2025-12-20 11:03:00,393[INFO] Step 41. Time 8.20. $n$ 0.8827020259679245
2025-12-20 11:03:00,409[INFO] Step 42. Time 8.40. $n$ 0.8796958667524066
2025-12-20 11:03:00,426[INFO] Step 43. Time 8.60. $n$ 0.8766726737398559
2025-12-20 11:03:00,442[INFO] Step 44. Time 8.80. $n$ 0.8736347299848458
2025-12-20 11:03:00,458[INFO] Step 45. Time 9.00. $n$ 0.8705861034366976
2025-12-20 11:03:00,475[INFO] Step 46. Time 9.20. $n$ 0.8675328737556515
2025-12-20 11:03:00,491[INFO] Step 47. Time 9.40. $n$ 0.8644830817098144
2025-12-20 11:03:00,508[INFO] Step 48. Time 9.60. $n$ 0.8614463370235249
2025-12-20 11:03:00,524[INFO] Step 49. Time 9.80. $n$ 0.8584330043902285

# plotting the occupation
from matplotlib import pyplot as plt
plt.style.use("mm.mplstyle")

plt.plot(np.arange(len(n_list)) * dt, n_list, label="Default")
plt.xlabel("$t$")
plt.ylabel(r"Occupation $\langle a^\dagger_0 a_0 \rangle$")
plt.legend()
plt.show()

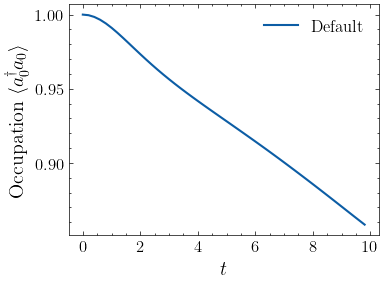
In this example, the time evolution is performed with default time evolution configuration and MPS compression configuration.

Renormalizer by default uses the RK4 “propagation and compression” method for time evolution. The advantage of the method is that it is easy to understand and setup.

Please refer to our recent review for a discussion of the different time evolution schemes.

mps.evolve_config.method

<EvolveMethod.prop_and_compress: 'P&C'>

Regarding MPS compression/truncation configuration, Renormalizer by default employs a truncation scheme based on the the singular value threshold.

mps.compress_config.criteria, mps.compress_config.threshold

(<CompressCriteria.threshold: 'threshold'>, 0.001)

Inspection of the dimension of the final mps after time evolution shows that the compression is efficient.

mps.bond_dims

[1, 2, 4, 1]

Configuring Time Evolution

In order to configure the time evolution, you should update the evolve_config and compress_config attributes of an MPS instance. These attributes are instances of the EvolveConfig class and the CompressConfig class. Please see the API referece for full options of the configuration classes.

from renormalizer.utils.configs import CompressConfig, CompressCriteria

# update the compresssion configuration. Adopt a fixed bond dimension of 8
mps.compress_config = CompressConfig(CompressCriteria.fixed, max_bonddim=8)

Next, we perform one more step of the time evolution, and the bond dimension in the middle of the MPS is increased from 4 to 8, according to the updated compression configuration.

new_mps = mps.evolve(mpo, dt)
new_mps.bond_dims

[1, 2, 8, 1]

Recent studies have shown that methods based on time dependent variantional principle (TDVP) show higher accuracy and efficiency. In our production runs, we usually employ one-site TDVP with projector splitting (TDVP-PS) for time evolution. TDVP-PS allows much larger time evolution step size and reduces memory consumption. However, its setup is a little more complex than propagation and compression, since one-site TDVP generally can not adjust bond dimension during time evolution.

from renormalizer.utils.configs import EvolveConfig, EvolveMethod

mps.evolve_config = EvolveConfig(EvolveMethod.tdvp_ps)

Next, we perform one more step of the time evolution using TDVP-PS.

Note that the bond dimension in the middle of the MPS does not increase from 4 to 8. This is because one-site TDVP-PS does not alter the bond dimension.

In order to perform one-site TDVP-PS time evolution, it is imperative to increase the bond dimension of the MPS first, and then perform the time evolution.

new_mps = mps.evolve(mpo, dt)
new_mps.bond_dims

[1, 2, 4, 1]

The expand_bond_dimension function increases the bond dimension to target value specified by the compress_config. In short, the function adds the vectors in the Krylov space \(H^n|\psi\rangle\) to the input wavefunction \(|\psi\rangle\), and then compresses it to the target bond dimension. expand_bond_dimension works with fixed bond dimension compression configuration, instead of singular value truncation threshold.

The include_ex option is specifically designed for systems with quantum number conservation. If the initial wavefunction does not include contributions from a certain symmetry sector, these contributions will not reappear during time evolution due to the projection error in TDVP. Setting include_ex=True will add a small perturbation to the initial state to help recover the missing symmetry sector contributions. In our case, the quantum number conservation is disabled, so we set include_ex=False.

new_mps = mps.expand_bond_dimension(mpo, include_ex=False)
new_mps.bond_dims

[1, 2, 8, 1]

Observing Marcus Inverted Region

Next, we put everything together and perform time evolution with different \(\Delta G\) using TDVP-PS. Since the initial state of time evolution is a Hartree product state, we must expand the bond dimension before performing the time evolution.

# time evolution step
dt = 0.5

# initialize the MPS in the Hartree product state
init_mps = Mps.hartree_product_state(model, condition=init_condition)
logger.info(f"Initial MPS bond dimension: {init_mps.bond_dims}")
# setup compression configuration
init_mps.compress_config = CompressConfig(CompressCriteria.fixed, max_bonddim=8)
# setup time evolution configuration
init_mps.evolve_config = EvolveConfig(EvolveMethod.tdvp_ps)


# record the electronic occupation
n_list_list = []

delta_g_list = np.linspace(0, -2, 5)
for delta_g in delta_g_list:
    # reconstruct the Hamiltonian. We can reuse the occupation operator though
    model = get_model(delta_g)
    mpo = Mpo(model)
    # since using TDVP-PS, expand the bond dimension to target value.
    # otherwise the time evolution is limited to the Hartree product state.
    mps = init_mps.expand_bond_dimension(mpo, include_ex=False)
    logger.info(f"MPS bond dimension after expanding: {mps.bond_dims}")
    n_list = []
    for i_step in range(20):
        n = mps.expectation(n_op)
        logger.info(f"Step {i_step}. Time {i_step * dt:.2f}. $n$ {n}")
        # perform time evolution. Note that the evolution is not in-place.
        mps = mps.evolve(mpo, dt)
        n_list.append(n)
    n_list_list.append(n_list)

2025-12-20 11:03:02,989[INFO] Initial MPS bond dimension: [1, 1, 1, 1]
2025-12-20 11:03:03,011[INFO] MPS bond dimension after expanding: [1, 2, 8, 1]
2025-12-20 11:03:03,013[INFO] Step 0. Time 0.00. $n$ 1.0
2025-12-20 11:03:03,039[INFO] Step 1. Time 0.50. $n$ 0.9975776788496084
2025-12-20 11:03:03,064[INFO] Step 2. Time 1.00. $n$ 0.9911341778211974
2025-12-20 11:03:03,089[INFO] Step 3. Time 1.50. $n$ 0.9824981838275654
2025-12-20 11:03:03,114[INFO] Step 4. Time 2.00. $n$ 0.9733283418283671
2025-12-20 11:03:03,140[INFO] Step 5. Time 2.50. $n$ 0.9645218516469742
2025-12-20 11:03:03,164[INFO] Step 6. Time 3.00. $n$ 0.956338236849222
2025-12-20 11:03:03,190[INFO] Step 7. Time 3.50. $n$ 0.948730433389221
2025-12-20 11:03:03,215[INFO] Step 8. Time 4.00. $n$ 0.9415533981894391
2025-12-20 11:03:03,240[INFO] Step 9. Time 4.50. $n$ 0.9346400325046197
2025-12-20 11:03:03,265[INFO] Step 10. Time 5.00. $n$ 0.9278351842220703
2025-12-20 11:03:03,290[INFO] Step 11. Time 5.50. $n$ 0.9210298996164082
2025-12-20 11:03:03,315[INFO] Step 12. Time 6.00. $n$ 0.91417498313307
2025-12-20 11:03:03,340[INFO] Step 13. Time 6.50. $n$ 0.9072563582422929
2025-12-20 11:03:03,365[INFO] Step 14. Time 7.00. $n$ 0.9002591286104608
2025-12-20 11:03:03,390[INFO] Step 15. Time 7.50. $n$ 0.8931521085342404
2025-12-20 11:03:03,415[INFO] Step 16. Time 8.00. $n$ 0.8858943878575142
2025-12-20 11:03:03,440[INFO] Step 17. Time 8.50. $n$ 0.8784553598367526
2025-12-20 11:03:03,465[INFO] Step 18. Time 9.00. $n$ 0.8708472420517188
2025-12-20 11:03:03,490[INFO] Step 19. Time 9.50. $n$ 0.8631616549410932
2025-12-20 11:03:03,534[INFO] MPS bond dimension after expanding: [1, 2, 8, 1]
2025-12-20 11:03:03,537[INFO] Step 0. Time 0.00. $n$ 1.0000000000000002
2025-12-20 11:03:03,562[INFO] Step 1. Time 0.50. $n$ 0.997540192587904
2025-12-20 11:03:03,587[INFO] Step 2. Time 1.00. $n$ 0.9906013628490229
2025-12-20 11:03:03,612[INFO] Step 3. Time 1.50. $n$ 0.9802488858640298
2025-12-20 11:03:03,637[INFO] Step 4. Time 2.00. $n$ 0.967659360810458
2025-12-20 11:03:03,663[INFO] Step 5. Time 2.50. $n$ 0.9537696503060081
2025-12-20 11:03:03,688[INFO] Step 6. Time 3.00. $n$ 0.939207294852096
2025-12-20 11:03:03,713[INFO] Step 7. Time 3.50. $n$ 0.9243586104260206
2025-12-20 11:03:03,738[INFO] Step 8. Time 4.00. $n$ 0.9094397848359155
2025-12-20 11:03:03,763[INFO] Step 9. Time 4.50. $n$ 0.8945511232283805
2025-12-20 11:03:03,788[INFO] Step 10. Time 5.00. $n$ 0.8797430038665824
2025-12-20 11:03:03,813[INFO] Step 11. Time 5.50. $n$ 0.8650797798247599
2025-12-20 11:03:03,838[INFO] Step 12. Time 6.00. $n$ 0.8506519218071079
2025-12-20 11:03:03,863[INFO] Step 13. Time 6.50. $n$ 0.8365374567180585
2025-12-20 11:03:03,888[INFO] Step 14. Time 7.00. $n$ 0.8227688239625945
2025-12-20 11:03:03,913[INFO] Step 15. Time 7.50. $n$ 0.8093300617593501
2025-12-20 11:03:03,938[INFO] Step 16. Time 8.00. $n$ 0.7961632960693849
2025-12-20 11:03:03,963[INFO] Step 17. Time 8.50. $n$ 0.7831685752085118
2025-12-20 11:03:03,988[INFO] Step 18. Time 9.00. $n$ 0.7702000677823142
2025-12-20 11:03:04,013[INFO] Step 19. Time 9.50. $n$ 0.7570646850987617
2025-12-20 11:03:04,058[INFO] MPS bond dimension after expanding: [1, 2, 8, 1]
2025-12-20 11:03:04,060[INFO] Step 0. Time 0.00. $n$ 1.0
2025-12-20 11:03:04,085[INFO] Step 1. Time 0.50. $n$ 0.9975277339592451
2025-12-20 11:03:04,111[INFO] Step 2. Time 1.00. $n$ 0.9904261839751383
2025-12-20 11:03:04,136[INFO] Step 3. Time 1.50. $n$ 0.9795268047068668
2025-12-20 11:03:04,161[INFO] Step 4. Time 2.00. $n$ 0.9659170449060821
2025-12-20 11:03:04,186[INFO] Step 5. Time 2.50. $n$ 0.9506850089406199
2025-12-20 11:03:04,211[INFO] Step 6. Time 3.00. $n$ 0.9347455146607817
2025-12-20 11:03:04,236[INFO] Step 7. Time 3.50. $n$ 0.9187422726641743
2025-12-20 11:03:04,262[INFO] Step 8. Time 4.00. $n$ 0.9030158921696063
2025-12-20 11:03:04,287[INFO] Step 9. Time 4.50. $n$ 0.8876520609099677
2025-12-20 11:03:04,312[INFO] Step 10. Time 5.00. $n$ 0.872598279802041
2025-12-20 11:03:04,337[INFO] Step 11. Time 5.50. $n$ 0.857774234254712
2025-12-20 11:03:04,362[INFO] Step 12. Time 6.00. $n$ 0.8431151893156008
2025-12-20 11:03:04,387[INFO] Step 13. Time 6.50. $n$ 0.8285809886892022
2025-12-20 11:03:04,411[INFO] Step 14. Time 7.00. $n$ 0.8141772509631204
2025-12-20 11:03:04,436[INFO] Step 15. Time 7.50. $n$ 0.7999687732355265
2025-12-20 11:03:04,461[INFO] Step 16. Time 8.00. $n$ 0.7860556760297769
2025-12-20 11:03:04,486[INFO] Step 17. Time 8.50. $n$ 0.7725203376680733
2025-12-20 11:03:04,511[INFO] Step 18. Time 9.00. $n$ 0.7593659426880244
2025-12-20 11:03:04,535[INFO] Step 19. Time 9.50. $n$ 0.7464615604976077
2025-12-20 11:03:04,579[INFO] MPS bond dimension after expanding: [1, 2, 8, 1]
2025-12-20 11:03:04,580[INFO] Step 0. Time 0.00. $n$ 1.0
2025-12-20 11:03:04,605[INFO] Step 1. Time 0.50. $n$ 0.9975406090105954
2025-12-20 11:03:04,630[INFO] Step 2. Time 1.00. $n$ 0.9906249611406741
2025-12-20 11:03:04,655[INFO] Step 3. Time 1.50. $n$ 0.9804700824710458
2025-12-20 11:03:04,679[INFO] Step 4. Time 2.00. $n$ 0.9686190882357237
2025-12-20 11:03:04,703[INFO] Step 5. Time 2.50. $n$ 0.95645066300393
2025-12-20 11:03:04,728[INFO] Step 6. Time 3.00. $n$ 0.9448244017405037
2025-12-20 11:03:04,752[INFO] Step 7. Time 3.50. $n$ 0.9339798618065533
2025-12-20 11:03:04,776[INFO] Step 8. Time 4.00. $n$ 0.9236970054402212
2025-12-20 11:03:04,802[INFO] Step 9. Time 4.50. $n$ 0.9136118419963748
2025-12-20 11:03:04,826[INFO] Step 10. Time 5.00. $n$ 0.9034945341198819
2025-12-20 11:03:04,850[INFO] Step 11. Time 5.50. $n$ 0.893329094055876
2025-12-20 11:03:04,875[INFO] Step 12. Time 6.00. $n$ 0.8832123669566796
2025-12-20 11:03:04,899[INFO] Step 13. Time 6.50. $n$ 0.8732206640791196
2025-12-20 11:03:04,923[INFO] Step 14. Time 7.00. $n$ 0.863341431359629
2025-12-20 11:03:04,948[INFO] Step 15. Time 7.50. $n$ 0.8534881635602944
2025-12-20 11:03:04,972[INFO] Step 16. Time 8.00. $n$ 0.8435889215797663
2025-12-20 11:03:04,997[INFO] Step 17. Time 8.50. $n$ 0.8336922458094265
2025-12-20 11:03:05,021[INFO] Step 18. Time 9.00. $n$ 0.8239993933202376
2025-12-20 11:03:05,046[INFO] Step 19. Time 9.50. $n$ 0.8147658344266686
2025-12-20 11:03:05,089[INFO] MPS bond dimension after expanding: [1, 2, 8, 1]
2025-12-20 11:03:05,091[INFO] Step 0. Time 0.00. $n$ 1.0000000000000002
2025-12-20 11:03:05,115[INFO] Step 1. Time 0.50. $n$ 0.9975784978846656
2025-12-20 11:03:05,139[INFO] Step 2. Time 1.00. $n$ 0.9911783314788777
2025-12-20 11:03:05,164[INFO] Step 3. Time 1.50. $n$ 0.9828793267407636
2025-12-20 11:03:05,188[INFO] Step 4. Time 2.00. $n$ 0.974804737510616
2025-12-20 11:03:05,212[INFO] Step 5. Time 2.50. $n$ 0.968100800824393
2025-12-20 11:03:05,237[INFO] Step 6. Time 3.00. $n$ 0.9626946118364352
2025-12-20 11:03:05,262[INFO] Step 7. Time 3.50. $n$ 0.9578334887382836
2025-12-20 11:03:05,286[INFO] Step 8. Time 4.00. $n$ 0.9528636883612422
2025-12-20 11:03:05,310[INFO] Step 9. Time 4.50. $n$ 0.9476402488995235
2025-12-20 11:03:05,334[INFO] Step 10. Time 5.00. $n$ 0.942371478319726
2025-12-20 11:03:05,358[INFO] Step 11. Time 5.50. $n$ 0.9372226613912163
2025-12-20 11:03:05,383[INFO] Step 12. Time 6.00. $n$ 0.9321434873912746
2025-12-20 11:03:05,407[INFO] Step 13. Time 6.50. $n$ 0.9270168710222653
2025-12-20 11:03:05,431[INFO] Step 14. Time 7.00. $n$ 0.9218472771188885
2025-12-20 11:03:05,456[INFO] Step 15. Time 7.50. $n$ 0.9167421622570109
2025-12-20 11:03:05,480[INFO] Step 16. Time 8.00. $n$ 0.9117276598161927
2025-12-20 11:03:05,505[INFO] Step 17. Time 8.50. $n$ 0.9066479717963627
2025-12-20 11:03:05,529[INFO] Step 18. Time 9.00. $n$ 0.901335514443374
2025-12-20 11:03:05,553[INFO] Step 19. Time 9.50. $n$ 0.8959335401185742

By plotting the figure, we see that when \(\Delta G=-1\), the charge transfer rate is highest.

t = np.arange(len(n_list_list[0])) * dt
for i, n_list in enumerate(n_list_list):
    label = r"$\Delta G =" + str(delta_g_list[i]) + "$"
    plt.plot(t, n_list, label=label, linestyle="--")
plt.xlabel("$t$")
plt.ylabel(r"Occupation $\langle a^\dagger_0 a_0 \rangle$")
plt.legend()

<matplotlib.legend.Legend at 0x7fc079dc6fd0>

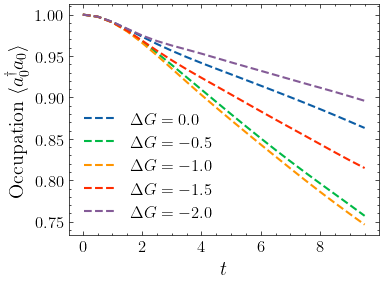
The prediction is consistent with the Marcus theory ,where the Marcus rate is

\[k = \frac{V^2}{\hbar} \sqrt{\frac{\pi\beta}{\lambda}} \exp{\left (-\frac{\beta(\lambda + \Delta G)^2}{4\lambda} \right )}\]

Here \(\lambda = 2g^2\omega = 1\) is the reorganization energy.

Features of Time Evolution Schemes

Renormalizer has a lot of different time evolution schemes, the most commonly used ones are 1. Propagation and Compression: EvolveMethod.prop_and_compress 2. Single-site TDVP-PS: EvolveMethod.tdvp_ps 3. Two-site TDVP-PS: EvolveMethod.tdvp_ps2 4. TDVP with varianble mean field (VMF): EvolveMethod.tdvp_vmf

The features of these methods are as follows

Name	Accuracy	Computational Cost	Adaptive Step-Size	Adaptive Bond Dimension	Projection Error
prop_and_compress	Low	High	partial	Yes	No
tdvp_ps	High	Low	No	No	Yes
tdvp_ps2	High	High	No	Yes	Partial
tdvp_vmf	High	High	Yes	No	Yes

“Adaptive Step-Size” refers to the ability to dynamically adjust the time-evolution step size based on a predefined error threshold. In practice, this means the method automatically takes smaller steps when the wavefunction changes abruptly and larger steps when it evolves smoothly. For example, tdvp_vmf performs multiple small steps within a single call to the evolve method. This capability removes the need for users to manually check step-size convergence in TD-DMRG by testing multiple step sizes.

“Adaptive Bond Dimension” refers to the ability to dynamically adjust the bond dimension during time evolution. Typically, the initial state is a Hartree product state. For tdvp_ps and tdvp_vmf, the expand_bond_dimension method should be called before starting the time evolution. Otherwise, the simulation will proceed with a bond dimension of 1 rather than the value specified in the optimization settings.

“Projection Error” is the error introduced when projecting the time derivative onto the MPS manifold.

Empirically, we recommend tdvp_ps for production level calculations.